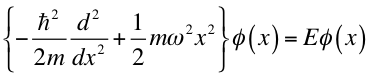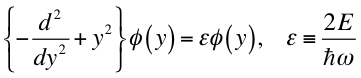STEP.08 [課題演習] 時間に依存しないシュレーディンガー方程式を解いてみる – 1次元調和振動子
ここでは、微分方程式の境界値問題を数値的に解く方法を、シュレディンガー方程式の定常解を例に解説します。
1次元調和振動子ポテンシャル V(x)=(1/2)mω2x2 中の質量 m の粒子を考えましょう。シュレディンガー方程式は、
と書けますが、変数変換
によって、無次元座標 y に関する次の方程式に変換できます。
この方程式の解の中で、y の遠方で波動関数が消える境界条件(φ(y ) → 0; y → ±∞)を満たすものを求めるにはどうすれば良いでしょうか。十分遠方をゼロとしてスタートして解を求めればよいように思われますが、一般の ε の値では、両端でゼロになるような境界条件を満たしません。境界条件を満たす特別な値(固有値) ε を決める必要があります。
01 反復法(iterative method)
ここでいう反復法とは、適当な固有値の試行値を使って微分方程式を解いてみて、その解が境界条件を満たしていなければ試行値を変えて積分をやり直すという操作を繰り返し、最終的に条件を満たす固有値の値とその波動関数を求める方法です。まず十分に大きな領域(例えば -5 ≤ y ≤ 5) を取って、座標 y を dy の刻みで離散化して、波動関数をその離散点 yn=n × dy で表現しましょう (例えば dy = 0.1、-50 ≤ n ≤ +50)。試行値の初期値を ε = 0 として、与えられた境界条件から左端 φ(–5) = 0 とします。そのすぐ隣の内側の点での値を適当に与えて、φ(–5+dy) = η として波動関数を y = +5 まで求めてみましょう。その右端での値の符号を調べます。εの値を少しずつ変化させて、波動関数の右端での値が符号を変える ε を求めます。
これでエネルギー固有値と定常状態の波動関数が求まったはずですが、波動関数をグラフにプロットしてみてください。束縛状態なので、右端で波動関数が小さくなっているべきですが、そうなっていないと思います。εの値として、1つ手前の値を使ってみると、今度は逆符号で大きな値を取っていると思います。これは、古典的に禁止される領域で上の微分方程式の2つの独立な解は、遠方でゼロになる解と発散する解の重ね合わせで、発散する成分を数値的に正確にゼロにするのは非常に困難なため、解を積分していくと、右端で発散する振る舞いを見せるのです。この問題を解決する一つの方法が次の射撃法(shooting method)と呼ばれる方法です。
02 射撃法(shooting method)
今度は左からだけでなく、右端からも解いて行きます。そして、ある点 y = y0 で左右から解いた解φL(y0), φR(y0) の値が同じになるように大きさを揃えます。シュレディンガー方程式は2階の斉次線形微分方程式なので、波動関数の大きさを全体で定数倍しても解であるという性質は変わりません。左右からの波動関数を合体させる点 y0 の取り方は原理的に任意ですが、転回点と呼ばれる古典的に許される領域と禁止される領域の境目に取ると数値的に比較的安定です。これは、ε– y2 = 0 で与えられるので、y = ±√ε のどちらかの点です(右でも左でも構いません)。転回点近傍で繋いだ解が求められたら、全体を規格化して、
としておきましょう。適当なεの値、例えばε = 0.5 の場合でまずこれをグラフにプロットしてみてください。左右の解を繋いだ点で明らかに「滑らか」になっていませんね。これが滑らかになるという条件が、固有値εを決める条件になります。この条件の付け方は色々ありますが、例えば、左からの解と右からの解が y = y0 の隣の点で一致するという条件で良いでしょう。つまり、次の値
η = φL(y0 – dy) – φR(y0 – dy)
が十分に小さくなるという条件です。ε の値を少しずつ増やしてみて、η の符号が変わる値を探しましょう。その値が近似的な固有値になります。もっと正確に求めたいときには、η = 0 となる値を2分法で求めてみるとよいでしょう。これで基底状態が求められました。ε = 1 が固有値、φ(y) = π–1/4 exp(-y2/2) が波動関数となっているはずです。さらに ε の値を増加させていけば、励起状態も全く同じようにして求めることができます。
ここまでできれば、調和振動子ポテンシャル以外の様々な1次元のポテンシャルに対して、束縛状態のエネルギーと波動関数を計算することができます。井戸型ポテンシャルで深さや幅を変えてみたり、色々とトライしてみましょう。