STEP.07 ポアソン方程式を解いてみる

ここでは、ポアソン方程式を数値的に解く方法について解説します。

01 1次元ポアソン方程式の差分化

次のような1次元のポアソン方程式を考えてみます。

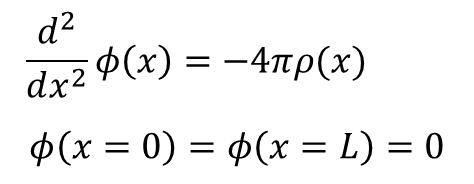
このポアソン方程式をコンピュータで解くために左辺の2階微分を次のように差分近似します。

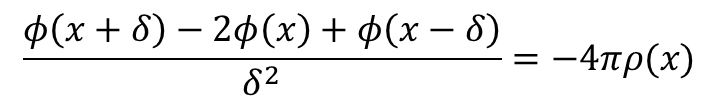
この式がポアソン方程式を差分近似していることは、左辺をテーラー展開することで確かめることがでます。
次に、下に示す図のようにx=0からx=Lまでの空間をN分割してxに番号を付けます。

分割の幅をδとすればxは

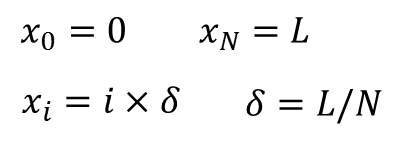
と書きあらわされます。この式を用いることで上の差分近似されたポアソン方程式を次のように書き直すことができます。

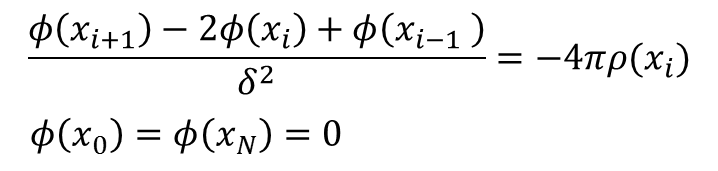
これで差分近似されたポアソン方程式を作ることができました。次に、この差分化された方程式の解をどのように見つけるかについて解説します。

02 ガウス・ザイデル法による求解

ここでは、上の差分化されたポアソン方程式を解くためにガウス・ザイデル法と呼ばれる方法について説明します。ガウス・ザイデル法の基本的な戦略は、近似的な解からさらに良い近似解を作る操作を何度も反復することで、最終的に真の解を得るというものです。近似解の更新は、差分化したポアソン方程式を変形した次の方程式を使います。

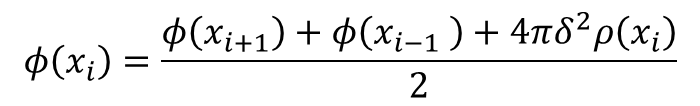
上の式を用いてポアソン方程式を解くプログラムを以下に模式的に示します。

上のプログラムではi=0,i=Nの点は除いて解の更新を行っています。これはi=0,i=Nにおける解の値が境界条件により決められているからです。また、例では最初の近似解として全空間にわたってφ=0を採用していますが、実際にはどんな値で計算しても構いません。
上の模式プログラムをもとにρ(x)=1/4πの場合のポアソン方程式を解くサンプル・プログラムを以下に示します。

program main
  implicit none
  integer,parameter :: N=50,M=50
  real(8),parameter :: pi=3.1415926535897932d0
  real(8) :: phi(0:N),rho(0:N)
  real(8) :: L,dx,x
  integer :: i,k

  rho=1d0/(4d0*pi)
  phi=0d0

  L=10d0
  dx=L/dble(N)

  do k=1,M

    do i=1,N-1
      phi(i)=(phi(i+1)+phi(i-1)+4d0*pi*dx**2*rho(i))/2d0
    end do

  end do


  open(10,file='poisson_result.out')
  do i=0,N
    x=i*dx
    write(10,'(3e16.6)')x,phi(i),rho(i)
  end do
  close(10)

end program main

原子核理論研究室