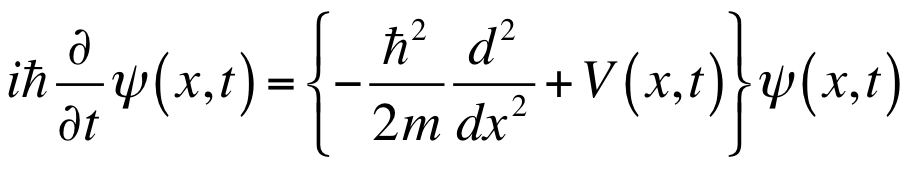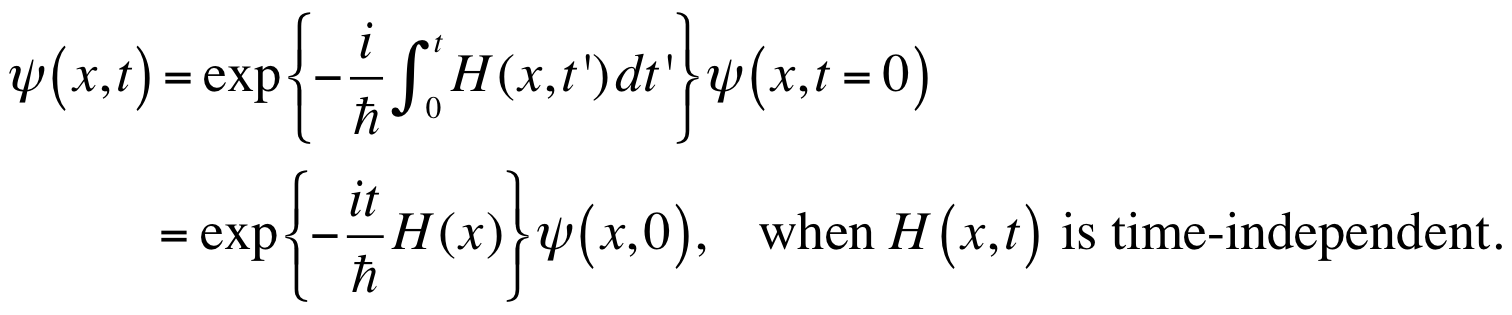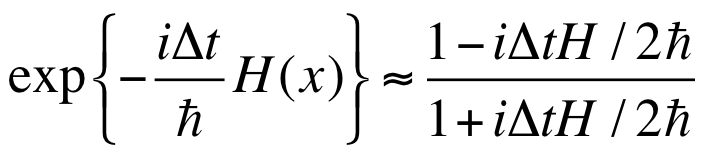STEP.09 [課題演習] 時間に依存するシュレーディンガー方程式を解いてみる – トンネル効果
ここでは、時間依存シュレディンガー方程式を解いて、波動関数の時間発展を求めます。計算のアルゴリズムは決して難しくありませんが、時間発展する波動関数は実数ではなく、どうしても複素数になることに注意しましょう。
一般に時間に依存するポテンシャル V(x,t) 中の質量 m の粒子に対する1次元の時間依存シュレディンガー方程式を考えます。
量子力学で良く知られているように、この解の波動関数のノルムは不変です。特にポテンシャルが時間に依存しない場合にはエネルギー期待値も保存します。これらを計算することで、数値的な時間発展の正しさをチェックすることができます。
まずは、ポテンシャルを時間に依存しない井戸型の斥力にして、
V(x) = V0 (for 0 < x < a), それ以外ではゼロ
としてみます。時刻 t = 0 での初期波動関数は、x = x0 < 0 に中心のあるガウス型の波束で exp(–(x-x0)2/2b2 + ikx) としてノルムを1に規格化しておきます。指数関数の中の第二項 ikx の部分によって、このガウス波束が波数 k > 0 の大きさの運動量で右に進む波にしてあります。やがて井戸型の斥力ポテンシャルに衝突するようにしてあります。ガウス波束の幅 b、波数 k、ポテンシャルの高さ V0 、幅 a などを色々と変化させてみると、量子トンネル現象の性質が解析できます。
01 テイラー展開を用いる
時間発展は形式的に以下のように書くことができます。
ハミルトニアンが時間に依存しない場合の下の式を見てください。指数関数は任意の大きさの時間刻みに分割することができます。
t = Δt × N
と N 分割して、Nを大きく取れば時間きざみ Δt を十分に小さくできるでしょう。そうすることで、指数関数 exp{…} 引数を1よりも十分に小さくしてやります。これで、t → t+Δt の微少時間発展は指数関数の展開で近似できるようになります。
展開の次数 M はΔt の大きさに依りますが、例えば M = 4 と取って、時間発展が十分正確に計算できるように Δt を決めてみましょう。Δt はもちろん可能な限り大きく取った方が計算は効率的です。このとき、ノルムやエネルギーの保存が指標になります。
初期のガウス波束は、原点よりも十分に左(x < 0 の領域)にあるようにパラメータ設定しましょう。井戸型ポテンシャルの高さ、幅を色々と変えてみましょう。
ここで、座標の刻み幅 dx を小さくしてみましょう。このとき、時間刻み Δt をどのように取るべきでしょうか?
02 Crank-Nicolson法
テイラー展開の方法は、有限次の展開で止めているために時間発展が厳密には「ユニタリー」ではなくなってしまいます。このために、長い時間発展の際には不安定性を引き起こす可能性があります。これに対して時間発展演算子を
と近似すると、少なくとも式の上ではユニタリー性が担保されます。この式を用いて、
ψ(x,t+Δt) = ψ(x,t) + u(x,t+Δt)
と置いて、u(x,t+Δt)が満たすべき方程式を導いてみましょう。u について非斉次2階線形微分方程式になると思います。これにはポアソン方程式を解いたときの方法を応用できそうです。このアルゴリズムは、有限差分法の精度を上げる方法の一つで、Crank-Nicolson法と呼ばれますものと同一です。