STEP.04 1階常微分方程式を解いてみる
コンピュータを使って微分方程式を解く方法について解説します。 微分方程式を解いた結果をすぐにグラフにして確認したいので、 以下の内容を読む前にgnuplotのインストールを参考にして、 グラフなどを描くためのソフトウェアであるGnuplotをインストールしておくことをお勧めします。
01 オイラー法
微分方程式を数値的に解くにあたって、まず始めにもっとも基本的なオイラー法と呼ばれる解き方について説明します。 次のような1階常微分方程式を解くことを考えてみましょう。
![]()
コンピュータを使って上の微分方程式を解くために、左辺の微分をStep.03の数値微分で行ったように差分で近似してみます。 すると、次のような漸化式を得ることができます。
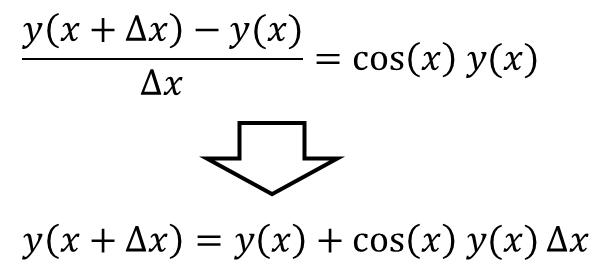
ここで得られた漸化式を次のような手順で用いることで、微分方程式を近似的に解くことができます。
手順 1
初期条件 y(0)=1 を用いて漸化式の右辺を計算しΔx 先のy(Δx)の値を求める。
手順 2
漸化式により計算された y(x) の値を用いて、さらに Δx 先の y(x+Δx) を求める。
手順 3
手順 2を適当な回数だけ繰り返す。
以上のような手順で数値的に微分方程式を解くことができます。
以下に上の微分方程式を x=0 から x=10 まで解き、その結果を出力するサンプル・コードを示します。 計算結果の出力とその可視化についてはその下で説明します。
program main implicit none integer i,N real(8) x,dx,y,true_y N=50 dx=10.0/N x=0 y=1.0 true_y=1.0 open(10,file='result.out') write(10,*)x,y,true_y do i=1,N y=y+cos(x)*y*dx x=dx*i true_y=exp(sin(x)) write(10,*)x,y,true_y end do close(10) end
上のコードは x=0 から x=1 0の区間をN分割し(つまりΔx=10/Nとして)先ほどの漸化式をN回使うことで、 微分方程式を近似的に解いています。 このプログラムは今までのサンプル・プログラムとは異なり、 計算結果を画面ではなく”result.out”という名前のファイルへ出力しています。
ファイルへの出力を行うために必要となるのが open文 です。サンプル・プログラムのように
open(10,file=’result.out’)
と書くことによってresult.outという名前のファイルが10番の番号に開かれます。 10番の番号で開かれたファイルに書き込むためには write(10,*)x,y,true_y というように、 writeの後のカッコで番号10を指定してください。 最後に、ファイルへの書き込みが終了したら close(10) のように10番の番号で開かれたファイルを閉じてください。
どの番号でファイルを開くかは基本的に自由に決めることができますが、 1ケタの番号は Error の出力などのために使用されている可能性があるので10以上の番号を指定してください。
これから数値計算を行なっていく上で、ファイルへの結果の書き出しは必須となります。 しっかりファイルへの出力の仕方を身につけましょう。次に、出力したファイルからグラフを作る方法について説明します。
02 計算結果の可視化-gnuplotの利用
長くなったので節を改めて、gnuplot を使って計算結果の可視化を行う方法について説明します。 上のプログラムを実行するとresult.out という名前のファイルに1列目に x 座標、2列目に x に対するyの値(数値計算の結果)、 3列目に x に対するyの値(真の解 y=exp{sin(x)}) が出力されています。
グラフを作るために、まず計算結果のファイルが置いてあるフォルダで gnuplot を起動しましょう。(起動の仕方はここを参照)
gnuplot が起動したら
plot “result.out” using 1:2 with line
と入力してみましょう。すると、先ほど計算した結果のグラフが描かれます。 さらに
plot “result.out” using 1:2 with line,”result.out” using 1:3 with line
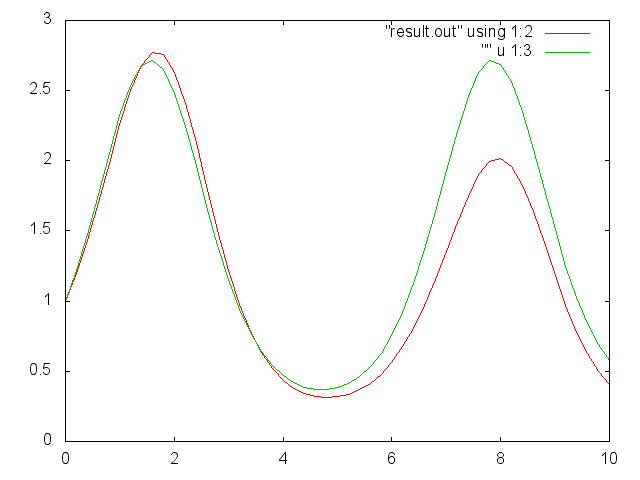
と入力すれば、下のように数値的に微分方程式を解いた結果に加えて解析的に解いた結果のグラフも描かれます。
上のgnuplotのコマンドを簡単に説明すると、plot の後に””でグラフにしたいファイルを選択し、 using で何行目の情報を使うか、with line で線グラフを指定してグラフを描いています。 より詳細な使い方については gnuplot tips などで調べてみましょう。
上のグラフを見ると、数値的に微分方程式を解いた結果と解析的に解いた結果がずれています。 プログラム中の分割数 N を変えて、数値計算の結果がどう変わるかを調べてみましょう。
03 より高精度な計算法-Runge-Kutta法
上で紹介したEuler法はもっとも基本的な微分方程式の解法です。 次により高精度な計算法である Runge-Kutta 法を簡単に紹介します。
1階の常微分方程式は一般的には次のように書くことができる。
![]()
この微分方程式を、次の漸化式によって解く方法が Runge-Kutta 法です。
![]()
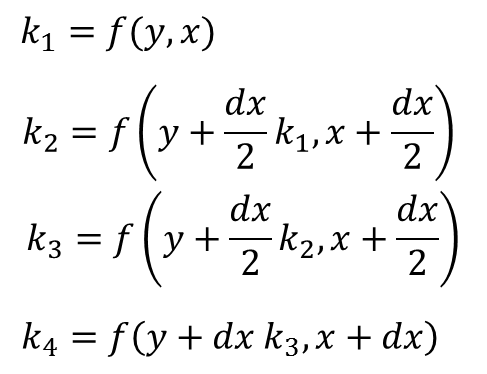
以下に先ほど Euler 法を用いて解いた微分方程式を Runge-Kutta 法を用いて解くサンプル・プログラムを示します。 先ほどの Euler 法の計算コードの時と同様に分割数 N を変えて、数値計算の結果がどう変わるかを調べてみましょう。
program main implicit none integer i,N real(8) x,dx,y,true_y real(8) k1,k2,k3,k4 N=50 dx=10.0/N x=0 y=1.0 true_y=1.0 open(10,file='result_R.out') write(10,*)x,y,true_y do i=1,N k1=cos(x)*y k2=cos(x+dx/2)*(y+k1*dx/2) k3=cos(x+dx/2)*(y+k2*dx/2) k4=cos(x+dx)*(y+k3*dx) y=y+dx/6*(k1+2*k2+2*k3+k4) x=dx*i true_y=exp(sin(x)) write(10,*)x,y,true_y end do close(10) end