STEP.05 2階常微分方程式を解いてみる – ニュートン方程式
いよいよ、Newton方程式をコンピュータを使って解く方法について解説していきます。 まずは簡単のために、次のような1次元のばねにつながれた質点の運動を解いていきましょう。
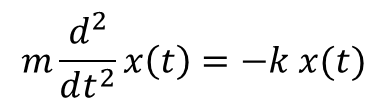
01 オイラー法でNewton方程式を解く
Newton方程式は2階の常微分方程式です。 したがって1階の常微分方程式であるオイラー法(STEP04で学んだ)を直接用いて解くことはできません。 オイラー法を用いて解くためには、まず2階の微分方程式を1階の連立微分方程式に書き直してやる必要があります。 といっても、それほど難しい書き換えではありません。 今回の場合は、速度 v(t) を導入することで、運動方程式を次のような1階の連立微分方程式に直すことができます。
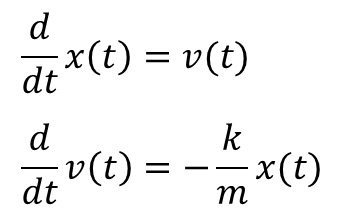
解きたい方程式が何回の微分方程式であろうと、上のような手続きを踏むことで1階の連立微分方程式へ書き直すことができます。
ここでは、上の連立微分方程式をオイラー法を用いて解いてみます。 オイラー法で微分方程式を解くためには、前回と同様にに次のような漸化式に従って逐次的に解を求めていきます。
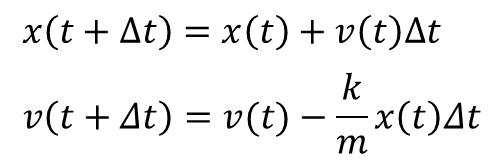
以下に、上の漸化式を用いて、初期条件 x(0)=1 , v(0)=0 における微分方程式の解を求めるサンプル・コードを示します。
program main
implicit none
real(8) x,v,f,t,dt,t_fin,x_old,v_old
integer Nt,it
real(8) m,k
t_fin=10d0
Nt=100
dt=t_fin/Nt
m=1d0
k=1d0
t=0d0
x_old=1d0
v_old=0d0
open(10,file='Newton_Euler.dat')
write(10,'(3e16.6E3)')t,x_old,v_old
do it=1,Nt
t=dt*it
x=x_old+v_old*dt
v=v_old-k/m*x_old*dt
x_old=x
v_old=v
write(10,*)t,x_old,v_old
end do
close(10)
end program main
計算結果が出たら、グラフを描いて見ましょう。 例えば、横軸を時間 t、縦軸を位置 x(t) として計算結果と解析解をプロットして比較を行ったり、 横軸を位置 x(t)、縦軸を速度 v(t) としてプロットして位相空間内での振る舞いを調べてみたりすると面白いでしょう。 また、これらのグラフが時間刻み幅Δtを変えるとどのように変化するのかを調べてみましょう。
02 Runge-Kutta法でNewton方程式を解く
上では Euler法を用いて Newton の運動方程式を解いていました。 しかし、前にも述べたように Euler法はもっとも単純な計算方法であり、精度が出にくいです。 そこで、Runge-Kutta法を用いて高精度に微分方程式を解く計算コードを書いてみましょう。
計算コードを書くために、まず Runge-Kutta法の漸化式を立てる必要があります。 連立微分方程式における Runge-Kutta法の漸化式をSTEP.04を参考に立ててみましょう。 漸化式が立ったら実際に計算コードを書き、計算結果と解析解、Euler法で解いた結果などを比較してみましょう。
以下に、参考のためのサンプル・コードを示しておきます。
program main
implicit none
real(8) x,v,f,t,dt,t_fin
integer Nt,it
real(8) m,k
real(8) kx1,kx2,kx3,kx4,kv1,kv2,kv3,kv4
t_fin=10d0
Nt=100
dt=t_fin/Nt
m=1d0
k=1d0
t=0d0
x=1d0
v=0d0
open(10,file='Newton_Runge_Kutta.dat')
write(10,'(3e16.6E3)')t,x,v
do it=1,Nt
t=dt*it
kx1=v
kv1=-k/m*x
kx2=v+kv1*dt/2
kv2=-k/m*(x+kx1*dt/2)
kx3=v+kv2*dt/2
kv3=-k/m*(x+kx2*dt/2)
kx4=v+kv3*dt
kv4=-k/m*(x+kx3*dt)
x=x+dt/6*(kx1+2*kx2+2*kx3+kx4)
v=v+dt/6*(kv1+2*kv2+2*kv3+kv4)
write(10,*)t,x,v
end do
close(10)
end program main
03 STEP.05のおわりに
ここでは1次元のバネの問題を例にニュートン方程式を数値的に解く方法について解説しましたが、他の問題でも基本的なところは変わりません。ここで学んだことを生かして、2、3次元の問題を計算するコードを書いたり、いくつかの粒子が相互作用しているような系の問題を解く計算コードを書いたりすることもできます。また、ここでは Euler法と Runge-Kutta法しか紹介できませんでしたが、 他にも計算方法は存在します。 蛙飛び法(leap-frog method)や Verlet法と呼ばれる方法がよく用いられているようです。 自ら調べて、様々な問題に挑戦してみましょう。

