STEP.03 数値微分・数値積分
いよいよ、ここから本格的な数値計算に入っていきます。 まずはコンピュータを使って微分や積分の計算を行ってみましょう。
01 数値微分
まずは微分の計算から練習していきましょう。
関数の微分は次の式によって定義されています。
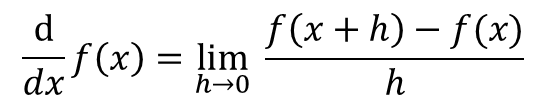
“本当の微分”は、微小量hが0の極限で定義されています。 しかし十分小さな h を使って上の式の分数を計算してやれば、近似的に関数の微分を計算してやることができます。 このような近似を「差分近似」と呼びます。 また、差分近似を用いて数値的に微分を行う操作が”数値微分”です。 数値微分は分数の計算を行うだけなので、加減乗除の四則演算ができれば簡単にプログラムを書くことができます。 以下に数値微分を行うサンプルプログラムを示します。
program main implicit none real(8) x,h,fx0,fx1,dfdx x=0.0 h=0.2 fx0=sin(x) fx1=sin(x+h) dfdx=(fx1-fx0)/h write(*,*)dfdx end
上のプログラムでは三角関数 sin(x) の x=0 における微分係数の計算を行っています。 行われている操作は単純です。 まず、fx0 に sin(x) の値、fx1 に sin(x+h) の値を代入しています。 次に、fx1, fx0 の差をhで割ったもの、つまり微分係数の近似値を計算して dfdx に代入します。 最後に、求めた微分の近似値 dfdx を出力しています。
sin(x) の x=0 における微分係数のは cos(0)=1 ですが、 プログラムを実行して得られる近似値はこの値に近いでしょうか? また、微小量hの大きさを変化させると近似値の値はどうなるでしょうか? いろいろ自分で試しながら練習してみてください。
02 数値積分
コンピュータを使った微分の計算ができるようになったので、 次はコンピュータを使った積分の計算に挑戦してみましょう。
左下の図のような関数 f(x) の x=a から x=b までの積分を考えてみましょう。 この積分の結果はちょうど赤斜線の面積と等しくなります。 つまりこの面積が求まれば積分できたことになります。
数値的に積分を行うための第一の手続きとして、 赤斜線の面積を右下図のような青斜線の台形の面積で近似してみます。
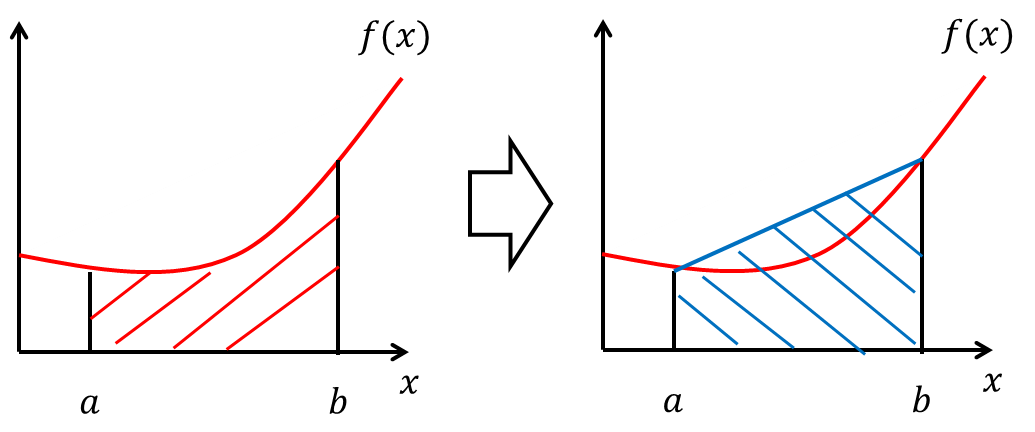
青斜線の面積は台形の面積の公式を用いると {f(a)+f(b)}(b-a)/2 と計算することができます。 しかしこのままでは図を見ても分かるように求めたい値との差が大きそうです。 そこで次の段階の近似として積分区間を等間隔に分割し、 それぞれの区間を上と同様に台形の面積で近似してみます。 積分区間を4等分した例を右下図に示しました。 1つの台形で近似していた時に比べて、求めたい面積をよく近似できているように見えます。
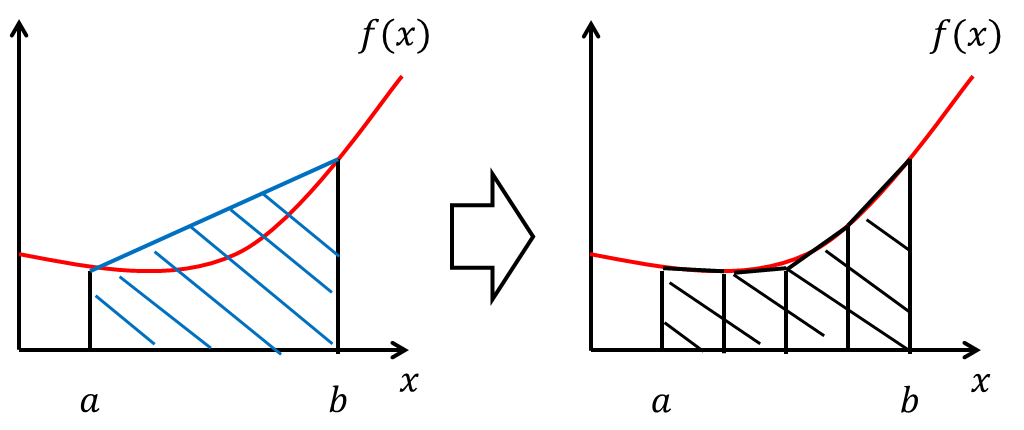
このように求めたい積分をN個の等間隔な区間に分割し、それぞれの区間の積分を台形の面積で近似した場合、 積分の近似値は次のような和で書き下すことができます。
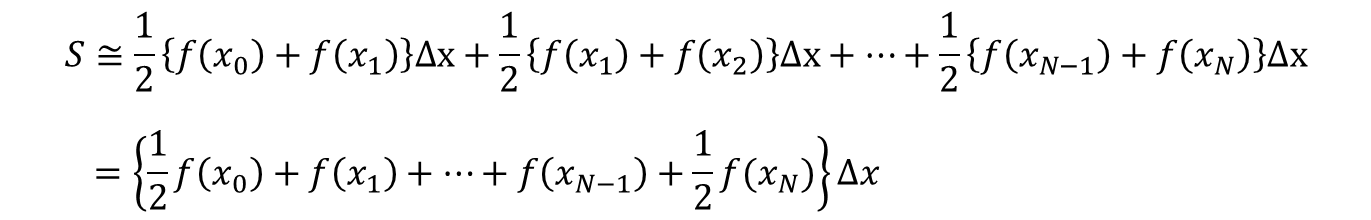
ただし、ここに現れている変数は次のように定義されています。
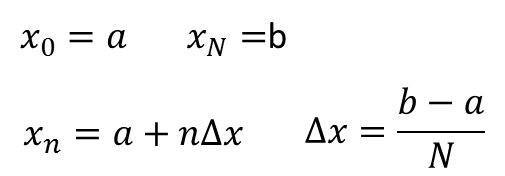
以下に、数値的に積分を行うサンプル・プログラムを示します。 このサンプル・プログラム参考にしながら、いろいろな関数の数値積分を実行してみましょう。 また、区間の分割数を変えると数値積分の結果と解析的に計算した(紙と鉛筆で計算した)結果の差がどうなるかを調べてみましょう。
program main implicit none integer i,N real(8) s,x,dx,a,b,f a=0.0 b=1.0 N=10 dx=(b-a)/N x=a s=0.5d0*exp(x) do i=1,N-1 x=a+dx*i s=s+exp(x) end do x=a+dx*N s=s+0.5d0*exp(x) s=s*dx write(*,*)'true =',exp(b)-exp(a) write(*,*)'calc =',s end
03 数値微分・数値積分の終わりに
このページでは数値微分・数値積分の基礎について解説しました。 ここで紹介した数値微分・数値積分の方法は最も基本的な方法であり、 より高い精度で数値微分・数値積分を行う計算方法があります。 意欲のある人は「数値微分」「数値積分」などをキーワードにして高精度の計算法について調べてみましょう。

